Proof Without Words: Trigonometric Differentiation
Is this some kind of “proof without words”?
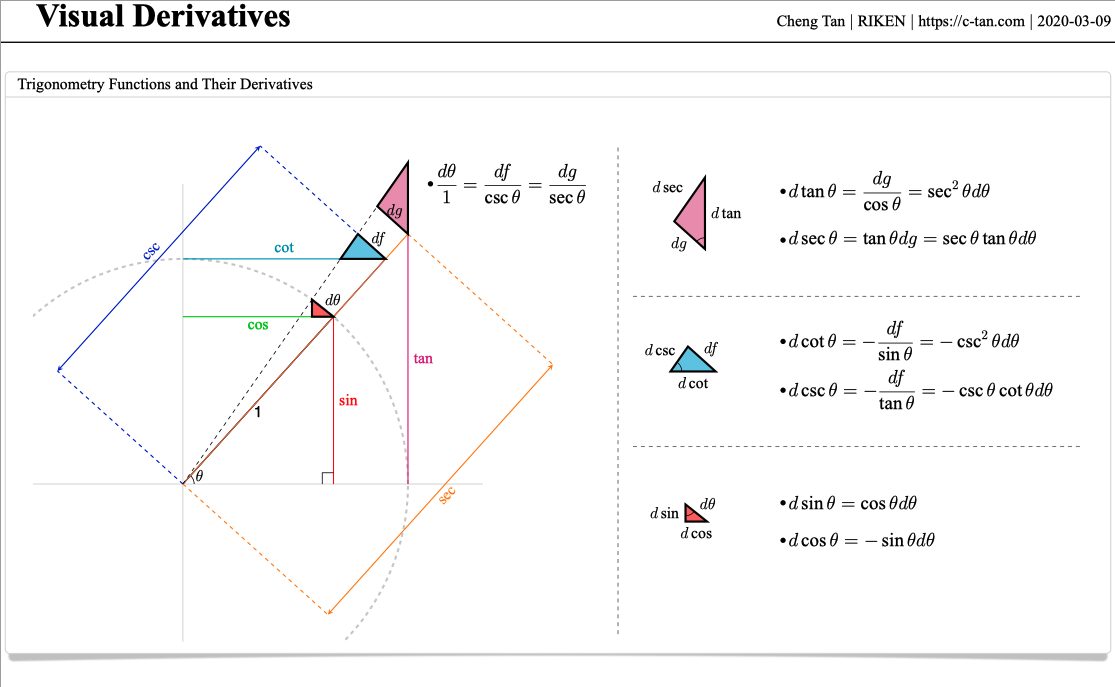
As usual, you can download the PDF version.
Plotted with this ugly code in the following (using TikZ ):
\def\radiusa{6.0}
\def\radiusb{0.3}
\def\radiusc{5.2}
\def\radiusd{4.5}
\def\desa{1.4}
\def\desb{1.4}
\def\anglea{48}
\def\angleb{138}
\def\anglec{-42}
\def\angleap{55}
\begin{tikzpicture}[x=1.0cm,y=1.0cm,font=\sffamily]
\clip (-4.0,-4.2) rectangle (24, 10);% 9 * 5
% \draw[help lines,step=1] (-5,-5) grid (22,12);
\draw [color=black!20,ultra thin] (-8, 0) -- (8, 0);
\draw [color=black!20,ultra thin] (0, -8) -- (0, 8);
\coordinate (O) at (0, 0);
\coordinate (A) at (\anglea:\radiusa);
\coordinate (Ap) at (\angleap:\radiusa);
\coordinate (App) at (\radiusa * cos \angleap, \radiusa * sin \anglea);
\coordinate (B) at (\radiusa * cos \anglea, 0);
\coordinate (C) at (0, \radiusa * sin \anglea);
\coordinate (D) at (\radiusa, 0);
\coordinate (E) at (0, \radiusa);
\coordinate (F) at (\radiusa, \radiusa * tan \anglea);
\coordinate (Fp) at (\radiusa, \radiusa * tan \angleap);
\coordinate (G) at (\radiusa * cot \anglea, \radiusa);
\coordinate (Gp) at (\radiusa * cot \angleap, \radiusa);
\coordinate (H) at (\radiusc * cos \anglec, \radiusc * sin \anglec);
\coordinate (I) at (\radiusd * cos \angleb, \radiusd * sin \angleb);
\coordinate (J) at (\radiusa * cot \anglea + \radiusd * cos \angleb, \radiusa + \radiusd * sin \angleb);
\coordinate (K) at (\radiusa + \radiusc * cos \anglec, \radiusa * tan \anglea + \radiusc * sin \anglec);
\coordinate (Ba) at (\radiusa * cos \anglea,\radiusb);
\draw [color=black!20,ultra thick,dashed] (O) circle (\radiusa);
\draw [color=black,thin] (0:\radiusb) arc(0:\anglea:\radiusb) node[right] {$\theta$};
\draw [color=black,thick] (O) -- (A) node[midway,below,black] {1};
\draw [color=red,thick] (A) -- (B) node[midway,right,red] {$\sin$};
\draw [color=green!80!black,thick] (C) -- (A) node[midway,below,green!80!black] {$\cos$};
\draw [color=magenta,thick] (D) -- (F) node[midway,right,magenta] {$\tan$};
\draw [color=cyan!80!black,thick] (E) -- (G) node[midway,above,cyan!80!black] {$\cot$};
\draw [color=blue!80!black,thick] (O) -- (G);
\draw [color=orange,thick] (O) -- (F);
\draw [color=blue!80!black,thick,dashed] (O) -- (I);
\draw [color=blue!80!black,thick,dashed,name path=lgj] (G) -- (J);
\draw [color=orange,thick,dashed] (O) -- (H);
\draw [color=orange,thick,dashed] (F) -- (K);
\draw [color=white,ultra thin,name path=lfk] (F) -- ++(\angleb:\radiusc);
\draw [color=blue!80!black,thick,stealth-stealth] (I) -- (J) node[sloped,midway,above,blue!80!black] {$\csc$};
\draw [color=orange,thick,stealth-stealth] (H) -- (K) node[sloped,midway,below,orange] {$\sec$};
\draw [color=black,thin] (Ba) -- ++(180:\radiusb) -- ++(270:\radiusb);
% theta + \delta theta
\draw [color=black,dashed,name path=lofp] (O) -- (Fp);
\draw [color=black,ultra thick,fill=red!60] (A)
-- (Ap) node[midway,above right=-3pt] {$d\theta$}
-- (App) -- cycle;
\fill [name intersections={of=lofp and lgj,name=Gpp}];
\draw [color=black,ultra thick,fill=cyan!50] (G) -- (Gp)
-- (Gpp-1) -- cycle node[midway,above right=-5pt] {$df$};
\fill [name intersections={of=lofp and lfk,name=Fpp}];
\draw [color=black,ultra thick,fill=magenta!50] (F) -- (Fp)
-- (Fpp-1) -- cycle;
\node at (5.65, 7.25) {$dg$};
\draw [color=black!50,thick,dashed] (11.6, -4) -- (11.6, 9);
% new triangle 1
\coordinate (NApp) at ($(13.4, -1)$);
\coordinate (NAp) at ($(Ap) - (App) + (NApp)$);
\coordinate (NA) at ($(A) -(App) + (NApp)$);
\draw [color=black,ultra thick,fill=red!60] (NA)
-- (NAp) node[midway,above right=-2pt] {$d\theta$}
-- (NApp) node[midway,left] {$d\sin$}
-- cycle node[midway,below] {$d\cos$};
\coordinate (NApt) at ($(NAp) + ( \radiusb * sin \anglea, - \radiusb * cos \anglea)$);
\draw [color=black,thin] (NApt) arc(\anglec:-90:\radiusb);
\draw [color=black!50,thick,dashed] (12, 1) -- (24, 1);
% new trangle 2
\coordinate (NGp) at ($(13.0, 3)$);
\coordinate (NG) at ($(G) - (Gp) + (NGp) $);
\coordinate (NGpp) at ($(Gpp-1) - (Gp) + (NGp)$);
\draw [color=black,ultra thick,fill=cyan!50] (NG)
-- (NGp) node[midway,below] {$d\cot$}
-- (NGpp) node[midway,above left=-2pt] {$d\csc$}
-- cycle node[midway,above right=-3pt] {$df$};
\coordinate (NGpt) at ($(NGp) + (\radiusb, 0)$);
\draw [color=black,thin] (NGpt) arc(0:\anglea:\radiusb);
\draw [color=black!50,thick,dashed] (12, 5) -- (24, 5);
% new trangle 3
\coordinate (NFpp) at ($(13.1, 7)$);
\coordinate (NFp) at ($(Fp) - (Fpp-1) + (NFpp)$);
\coordinate (NF) at ($(F) - (Fpp-1) + (NFpp)$);
\draw [color=black,ultra thick,fill=magenta!50] (NF)
-- (NFp) node[midway,right] {$d\tan$}
-- (NFpp) node[midway,above left] {$d\sec$}
-- cycle node[midway,below left=-3pt] {$dg$};
\coordinate (NFt) at ($(NF) + (0, \radiusb)$);
\draw [color=black,thin] (NFt) arc(90:\angleb:\radiusb);
% NOTES
\fill (6.6, 8) circle (2pt) node [right] {\large $\displaystyle \frac{d\theta}{1} = \frac{df}{\csc \theta} = \frac{dg}{\sec \theta}$};
\fill (16, -1.5) circle (2pt) node [right] {\large $d\cos\theta = -\sin\theta d\theta$};
\fill (16, -0.5) circle (2pt) node [right] {\large $d\sin\theta = \cos\theta d\theta$};
\fill (16, 3.8) circle (2pt) node [right] {\large $\displaystyle d\cot\theta = -\frac{df}{\sin\theta} = -\csc^2\theta d\theta$};
\fill (16, 2.5) circle (2pt) node [right] {\large $\displaystyle d\csc\theta = -\frac{df}{\tan \theta} = -\csc\theta \cot\theta d\theta$};
\fill (16, 6.5) circle (2pt) node [right] {\large $\displaystyle d\sec\theta = \tan\theta dg = \sec\theta \tan\theta d\theta$};
\fill (16, 7.8) circle (2pt) node [right] {\large $\displaystyle d\tan\theta = \frac{dg}{\cos \theta} = \sec^2\theta d\theta$};
\end{tikzpicture}
Happy $\LaTeX$ing!